Question

Which equation has a graph that lies entirely above the x-axis?

Oy= -(x + 7)2 + 7
O y=(x-77²-7
y = (x – 7)2 + 7
y = (x – 7)

Answer 1

Option C.

Explanation:

The vertex form of a parabola is

`y=a(x-h)^2+k`

where, a is constant, (h,k) is vertex.

If a<0, then it is a downward parabola and if a>0, then it is an upward parabola.

A downward parabola never lies entirely above the x-axis.

First equation is

`y=-(x+7)^2+7`

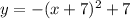
It is a downward parabola and vertex is (-7,7).

Second equation is

`y=(x-7)^2-7`

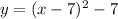
It is an upward parabola and vertex is (7,-7).

Third equation is

`y=(x-7)^2+7`

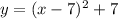
It is an upward parabola and vertex is (7,7).

Fourth equation is

`y=(x-7)`

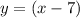
It is a linear equation with y-intercept -7.

Only equation 3 is an upward parabola whose vertex lies above the x-axis.

Hence the correct option is C.

Answer 2

• y =
  `(x-7)^(2)` + 7

Explanation:

The graph that will lie above the x-axis will be having only positive values throughout its domain,

So, We have to check which graph is having y > 0 for every x.

• y = -
  `(x+7)^(2)` + 7

clearly y will be negative for many values of x , as coefficient of variable is negative.

• y =
  `(x-7)^(2)` - 7

Put x = 0, you will get y as negative .

• y =
  `(x-7)^(2)` + 7

Since, Square of anything will always be positive , and here constant term is also positive , so, It will always be positive .

Thus, it is having its graph always above x axis.

• y = x - 7

Put x = 0 , y = -7, which is negative