Answer: No, It does not indicates that the population proportion of consumers loyal to Chevrolet is more than 47%.
Explanation:
Let p denotes the proportion of consumers loyal to Chevrolet.
As per given , we have
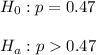
Since the alternative hypothesis
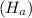 is right-tailed so the test would be a right-tailed test.
is right-tailed so the test would be a right-tailed test.
Also , it is given that ,Chevrolet did a study of a random sample of 1006 Chevrolet owners and found that 490 said they would buy another Chevrolet.
i.e. n = 1006
x= 490
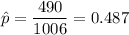
Test statistic :
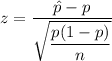
, where p=population proportion.
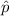 = sample proportion
= sample proportion
n= sample size.
i.e.
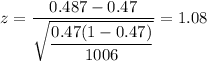
P-value (for right-tailed test)= P(z>1.08)=1-P(z≤1.08) [∵P(Z>z)=1-P(Z≤z)]
=1- 0.8599=0.1401 [By z-value table.]
Decision : Since p-value (0.14) is greater than the significance level (
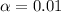 ) , it means we are failed to reject the null hypothesis.
) , it means we are failed to reject the null hypothesis.
Conclusion : We have sufficient evidence to support the claim that about 47% of the general consumer population in the United States is loyal to the automobile manufacturer of their choice.
Hence, it does not indicates that the population proportion of consumers loyal to Chevrolet is more than 47%.