Question

Limit as x approaches 0 of (2e^x-2)/x

Answer 1

Step-by-step explanation:

`\lim_(x \to \ 0) (2e^x-2)/(x)`

So first, we have to plug in zero and see if we can evaluate this limit simply from that.

When we plug in zero we get: (2e^0-2)/0

e^0 is 1 so we have 2-2/0 or 0/0. So we have an indeterminate form type 0/0.

This means we have to apply L'Hospital's Rule.

As a reminder L'Hospitals Rule is
`\lim_(x\to \ c) (f'(x))/(g'(x))`

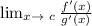
Meaning that we take the derivative of the top and bottom function as the approach some value "c". We can do this with a 0/0 indeterminate form.

So:

The derivative of 2e^x - 2 is just 2e^x

and the derivative of x is 1

So we are left with
`\lim_(x \to \ 0) 2e^x`

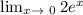
Plugging in zero we see this gives us 2 as 2(e^0) = 2(1) = 2.

Hence,
`\lim_(x \to \ 0) (2e^x-2)/(x)` = 2