Question

Marwick Corporation issues 8%, 5 year bonds with a par value of $1,200,000 and semiannual interest payments. On the issue date, the annual market rate for these bonds is 6%. What is the bond's issue (selling) price, assuming the following Present Value factors:

Answer 1

The selling price of the bonds is $1,302,362.43

Step-by-step explanation:

Hi, in order to find the present value of the bonds, we need to use the following formula.

`Price=(Coupon((1+Yield)^(n)-1) )/(Yield(1+Yield)^(n) ) +(FaceValue)/((1+Yield)^(n) )`

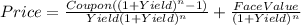
Where:

Coupon = the semi-annual interest payment (1,200,000*(8%/2)=48,000)

Yield = Annual market rate (2.96%)

n = Number of semi-annual payments (5 years*2 = 10 semesters)

Let me show you how to convert an effective annual rate (annual market rate) into a semi-annual effective rate.

`r(semi-annual)=(1+r(annual))^(1/2) -1`

`r(semi-annual)=(1+0.06)^(1/2) -1=0.029563`

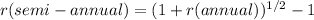
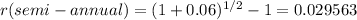
Everything should look like this.

`Price=(48,000((1+0.029563)^(10)-1) )/(0.029563(1+0.029563)^(10) ) +(1,200,000)/((1+0.029563)^(10) )`

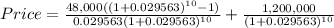
Therefore, the price is $1,307,074.18

Best of luck