Question

Consider an unreliable communication channel that can successfully send a message with probability 1/2, or otherwise, the message is lost with probability 1/2. How many times do we need to transmit the message over this unreliable channel so that with probability 63/64 the message is received at least once? Explain your answer.

Hint: treat this as a Bernoulli process with a probability of success 1/2. The question is equivalent to: how many times do you have to try until you get at least one success?

Answer 1

6 times we need to transmit the message over this unreliable channel so that with probability 63/64.

Explanation:

Consider the provided information.

Let x is the number of times massage received.

It is given that the probability of successfully is 1/2.

Thus p = 1/2 and q = 1/2

We want the number of times do we need to transmit the message over this unreliable channel so that with probability 63/64 the message is received at least once.

According to the binomial distribution:

`P(X=x)=(n!)/(r!(n-r)!)p^rq^(n-r)`

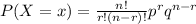
We want message is received at least once. This can be written as:

`P(X\geq 1)=1-P(x=0)`

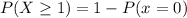
The probability of at least once is given as 63/64 we need to find the number of times we need to send the massage.

`(63)/(64)=1-(n!)/(0!(n-0)!)(1)/(2)^0(1)/(2)^(n-0)`

`(63)/(64)=1-(n!)/(n!)(1)/(2)^(n)`

`(63)/(64)=1-(1)/(2)^(n)`

`(1)/(2)^(n)=1-(63)/(64)`

`(1)/(2)^(n)=(1)/(64)`

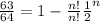
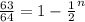
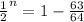
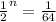
By comparing the value number we find that the value of n should be 6.

Hence, 6 times we need to transmit the message over this unreliable channel so that with probability 63/64.