Answer:
D
Explanation:
Quadratic has a general form of:
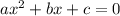
The quadratic given here is:

Matching it with the general form, we can see that:
a = 1 [coefficient of x^2]
b = 3
c = 1
Now, if we look at the formula for axis of symmetry, we can easily solve this out. The axis of symmetry is given by:
Axis of Symmetry is
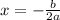
We know a = 1 and b = 3, so we have:
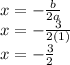
Hence,
D is the correct answer.