Question

A metal beam was brought from the outside cold into a machine shop where the temperature was held at 65degreesF. After 5 ​min, the beam warmed to 35degreesF and after another 5 min it was 50degreesF. Use​ Newton's Law of Cooling to estimate the​ beam's initial temperature.

Answer 1

The beam initial temperature is 5 °F.

Explanation:

If T(t) is the temperature of the beam after t minutes, then we know, by Newton’s Law of Cooling, that

`T(t)=T_a+(T_0-T_a)e^(-kt)`

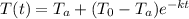
where
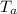`T_a` is the ambient temperature,
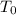`T_0` is the initial temperature,
`t` is the time and
`k` is a constant yet to be determined.

The goal is to determine the initial temperature of the beam, which is to say
`T_0`

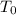
We know that the ambient temperature is
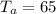`T_a=65`, so

`T(t)=65+(T_0-65)e^(-kt)`

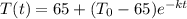
We also know that when
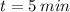`t=5 \:min` the temperature is
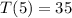`T(5)=35` and when
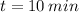`t=10 \:min` the temperature is
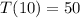`T(10)=50` which gives:

`T(5)=65+(T_0-65)e^(k5)\\35=65+(T_0-65)e^(-k5)`

`T(10)=65+(T_0-65)e^(k10)\\50=65+(T_0-65)e^(-k10)`

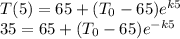
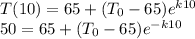
Rearranging,

`35=65+(T_0-65)e^(-k5)\\35-65=(T_0-65)e^(-k5)\\-30=(T_0-65)e^(-k5)`

`50=65+(T_0-65)e^(-k10)\\50-65=(T_0-65)e^(-k10)\\-15=(T_0-65)e^(-k10)`

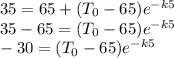
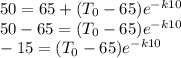
If we divide these two equations we get

`(-30)/(-15)=((T_0-65)e^(-k5))/((T_0-65)e^(-k10))`

`(-30)/(-15)=(e^(-k5))/(e^(-k10))\\2=e^(5k)\\\ln \left(2\right)=\ln \left(e^(5k)\right)\\\ln \left(2\right)=5k\ln \left(e\right)\\\ln \left(2\right)=5k\\k=(\ln \left(2\right))/(5)`

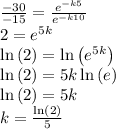
Now, that we know the value of
`k` we can use it to find the initial temperature of the beam,

`35=65+(T_0-65)e^{-((\ln \left(2\right))/(5))5}\\\\65+\left(T_0-65\right)e^{-\left((\ln \left(2\right))/(5)\right)\cdot \:5}=35\\\\65+(T_0-65)/(e^(\ln \left(2\right)))=35\\\\(T_0-65)/(e^(\ln \left(2\right)))=-30\\\\(\left(T_0-65\right)e^(\ln \left(2\right)))/(e^(\ln \left(2\right)))=\left(-30\right)e^(\ln \left(2\right))\\\\T_0=5`

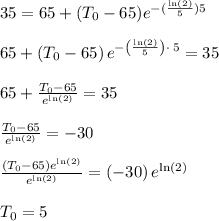
so the beam started out at 5 °F.