Question

Solve: In 2x + In 2 = 0
DONE

Answer 1

`x=(1)/(4)`

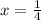
Explanation:

We can use some logarithmic rules to solve this easily.

Note: Ln means
`Log_e`

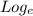
Now, lets start with the equation:

`ln(2x) + ln(2) = 0\\ln(2x) = -ln(2)`

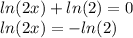
Writing left side with logarithmic base e, we have:

`Log_(e)(2x) = -ln(2)`

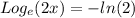
We can now use the property shown below to make this into exponential form:

`Log_(a)b=x\\means\\a^x=b`

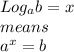
So, we write:

`Log_(e)(2x) = -ln(2)\\e^(-ln(2))=2x`

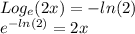
We recognize another property of exponentials:

`a^(bc)=(a^(b))^(c)`

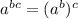
So, we write:

`e^(-ln(2))=2x\\(e^(ln(2)))^(-1)=2x`

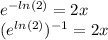
Also, another property of natural logarithms is:

`e^((ln(a)))=a`

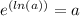
Now, we simplify:

`(e^(ln(2)))^(-1)=2x\\(2)^(-1)=2x\\(1)/(2)=2x\\x=((1)/(2))/(2)\\x=(1)/(4)`

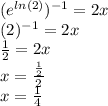
This is the answer.