Question

50 point for this question:

Find values of a and b that make the following equality into identity:

Answer 1

1) The values of 'a' and 'b' are
`$ (3)/(4) $` and
`$ (3)/(4) $` respectively.

2) The values of 'a' and 'b' are '3' and '-3' respectively.

Explanation:

1) Given:
`$ (3x)/((x - 2)(3x + 2)) = (a)/(x - 2) + (b)/(3x + 2) $`

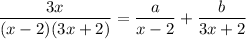
We solve this by partial fraction method.

Taking LCM in the RHS we get,

`$ (3x)/((x - 2)(3x + 2)) = (a(3x + 2) + b(x - 2))/((x - 2)(3x + 2)) $`

`$ \implies 3x = a(3x + 2) + b(x - 2) $`

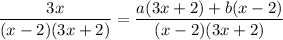
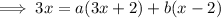
To find the value of 'a', substitute x = 2. This would make 'b' vanish leaving an equation with 'a'.

`$ \therefore 3(2) = a(3.2 + 2) + b (2 - 2) \implies 6 = a(8) $`

`$ \implies a = (-2)/(3) $`

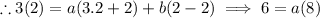
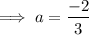
Now, Substitute
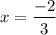`$ x = (-2)/(3) $` to solve for 'b'.

`$ \implies 3((-2)/(3)) = a (3.(-2)/(3) + 2) + b((-2)/(3) -2) $`

`$ \implies -2 = b (-8)/(3) $`

`$ \implies b = (3)/(4) $`

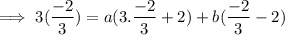
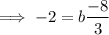
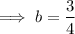
Therefore, a =
`$ (3)/(4) $` and b =
`$ (3)/(4) $`

2) Given
`$ (3)/(x^2 - 5x + 6) = (a)/(x - 2) + (b)/(x - 3) $`

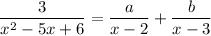
We follow the same procedure as (1).

Taking LCM we get

`$ (3)/(x^2 - 5x + 6) = (a (x - 3) + b(x - 2))/((x^2 - 5x + 6)) $`

`$ \implies 3 = a(x - 3) + b(x - 2) $`

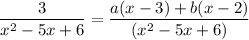
Substituting x = 2, we get:

3 = a(-1)
`$ \implies a = -3 $`

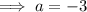
Also, Substituting x = 3, we get:

3 = b(1)

`$ \implies b = 1 $`

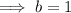
Therefore, the values of a and b are -1 and 1 respectively.