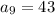Question

Consider the sequence:

3 , 8 , 13 , 18 , 23....

The recursive formula for this sequence is:


`a_(n) =a_(n-1) +5.`

In complete sentences, explain what
`a_(n),a_(n-1),` and the 5 represnt in the formula. Find
`a_(g)`. What do you need to know in order to find
`a_(g)` ?

Answer 1

The
`a_n` reprsents the nth term where n is some positive whole number {1,2,3,...}

The
`a_(n-1)` represents the term just before the nth term. For example, if n = 22 then
`a_(n) = a_(22)` and
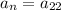`a_(n-1) = a_(21)`

The +5 at the end means we add 5 to the previous term just before the nth term to get the nth term. In other words, the rule is "add 5 to each term to get the next term".

To get the 9th term
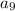`a_(9)`, we need to find the terms before this one because the recursive sequence builds up. The 9th term depends on the 8th term, which depends on the 7th term, and so on. The countdown stops until you reach the first term.

-------

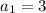`a_(1) = 3` (given)

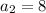`a_(2) = 8` (given)

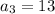`a_(3) = 13` (given)

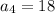`a_(4) = 18` (given)

`a_(5) = 23` (given)

`a_(6) = a_(5)+5 = 23+5 = 28` (add 5 to the prior term)

`a_(7) = a_(6)+5 = 28+5 = 33`

`a_(8) = a_(7)+5 = 33+5 = 38`

`a_(9) = a_(8)+5 = 38+5 = 43`

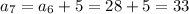
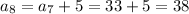
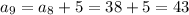
So the 9th term is
`a_(9) = 43`