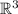Question

Apply the Gram-Schmidt orthonormalization process to transform the given basis for Rn into an orthonormal basis. Use the Euclidean inner product on Rn and use the vectors in the order in which they are given. B = {(8, −6, 0), (5, 1, 0), (0, 0, 2)}U1=??U2=??U3=??

Answer 1

Remember, if
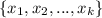`\{x_1,x_2,...,x_k\}` is a basis for a subspace W of
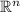`\mathbb{R}^n` then
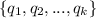`\{q_1,q_2,...,q_k\}` is an orthonormal basis of W, where

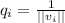`q_i=(1)/(||v_i||)` and
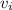`v_i` is defined as:

`v_1=x_1\\v_2=x_2-(v_1\cdot x_2)/(v_1\cdot v_1)v_1\\v_k=x_k-(v_1\cdot x_k)/(v_1\cdot v_1)v_1 - \cdots - (v_(k-1)\cdot x_k)/(v_(k-1)\cdot v_(k-1))v_(k-1)`

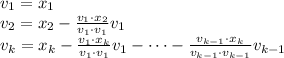
Then, to find a orthonormal basis of
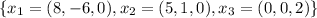`\{x_1=(8, -6, 0), x_2=(5, 1, 0), x_3=(0, 0, 2)\}` we will find first the
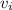`v_i`'s.

`v_1=x_1`

`v_2=x_2-(v_1\cdot x_2)/(v_1\cdot v_1)v_1=(5,1,0)-((8,-6,0)\cdot (5,1,0))/((8,-6,0)\cdot (8,-6,0))(8,-6,0)=\\=(5,1,0)-(17)/(50)(8,-6,0)=((57)/(25),(76)/(25),0)`

`v_3=x_3-(v_1\cdot x_3)/(v_1\cdot v_1)v_1-(v_2\cdot x_3)/(v_2\cdot v_2)v_2=\\=(0,0,2)-((8-6,0)\cdot (0,0,2))/((8,-6,0)\cdot (8,-6,0))(8,-6,0) -(((57)/(25),(76)/(25),0)\cdot (0,0,2))/(((57)/(25),(76)/(25),0)\cdot ((57)/(25),(76)/(25),0))((57)/(25),(76)/(25),0)=\\=(0,0,2)-0-0=\\=(0,0,2)`

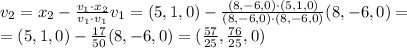
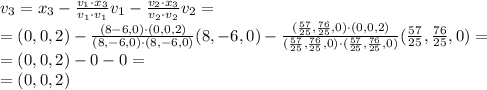
Therefore,
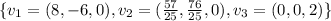`\{v_1=(8,-6,0),v_2=((57)/(25),(76)/(25),0),v_3=(0,0,2)\}` is a ortogonal basis for
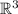`\mathbb{R}^3`. But we need a orthonormal basis. Then is enough find the corresponding unit vector of the ortogonal basis found.

`q_1=(1)/(||v_1||)v_1=(1)/(√(100))(8,-6,0)\\q_2=(1)/(||v_2||)v_2=(1)/((19)/(5))((57)/(25),(76)/(25),0)=(5)/(19)((57)/(25),(76)/(25),0)\\q_3=(1)/(||v_3||)v_3=(1)/(2)(0,0,2)`

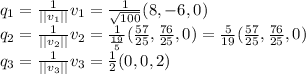
Hence

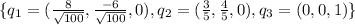`\{q_1=({(8)/(√(100)),(-6)/(√(100)),0), q_2=((3)/(5),(4)/(5),0), q_3=(0,0,1)\}` is a orthonormal basis for
`\mathbb{R}^3`