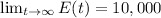Question

The projected rate of increase in enrollment at a new branch of the UT-system is estimated by E ′ (t) = 12000(t + 9)−3/2 where E(t) is the projected enrollment in t years.

If the inital enrollment is 2000, determine the projected enrollment after many years by calculating the value of lim t→ [infinity] E(t).

Answer 1

The projected enrollment is
`\lim_(t \to \infty) E(t)=10,000`

Explanation:

Consider the provided projected rate.

`E'(t) = 12000(t + 9)^{(-3)/(2)}`

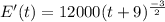
Integrate the above function.

`E(t) =\int 12000(t + 9)^{(-3)/(2)}dt`

`E(t) =-\frac{24000}{\left(t+9\right)^{(1)/(2)}}+c`

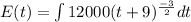
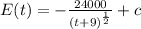
The initial enrollment is 2000, that means at t=0 the value of E(t)=2000.

`2000=-\frac{24000}{\left(0+9\right)^{(1)/(2)}}+c`

`2000=-(24000)/(3)+c`

`2000=-8000+c`

`c=10,000`

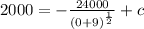
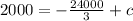
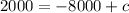
Therefore,
`E(t) =-\frac{24000}{\left(t+9\right)^{(1)/(2)}}+10,000`

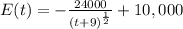
Now we need to find
`\lim_(t \to \infty) E(t)`

`\lim_(t \to \infty) E(t)=-\frac{24000}{\left(t+9\right)^{(1)/(2)}}+10,000`

`\lim_(t \to \infty) E(t)=10,000`

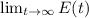
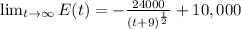
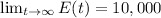
Hence, the projected enrollment is
`\lim_(t \to \infty) E(t)=10,000`