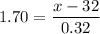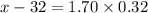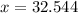Question

The weights of bags of baby carrots are normally distributed, with a mean of 32 ounces and a standard deviation of 0.32 ounce. Bags in the upper 4.5% are too heavy and must be repackaged. What is the most a bag of baby carrots can weigh and not need to be repackaged?

Answer 1

`x= 32.544`

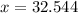
Step-by-step explanation:

given,

mean weight of bag (μ) = 32

standard deviation (σ) = 0.32

percentage of bag heavier = 4.5%

weight of the bag less than 4.5 % = 100 - 4.5

= 95.5%

we have to determine the z- value according to 95.5% or 0.955

using z-table

z-value = 1.70

now, using formula

`Z = (x-\mu)/(\sigma)`

`1.70 = (x-32)/(0.32)`

`x-32 = 1.70* {0.32}`

`x= 32.544`