The researcher would need a sample size of 271 individuals to be 90% confident that the sample proportion will not differ from the true proportion of adults
How to find the sample size ?
To determine the sample size needed to estimate the proportion of the adult population of the United States with high blood pressure with a 90% confidence level and a margin of error (precision) of 5%, you can use the formula for sample size for estimating proportions. The formula is:
![\[n = (Z^2 \cdot p(1-p))/(E^2)\]](https://img.qammunity.org/2020/formulas/mathematics/college/plqinmb5jgdiomr2gdxz0q09zuuzguj76u.png)
E is the margin of error as a proportion (in this case, 5% or 0.05).
Plug in the values:

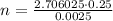
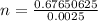
n = 270.6025
= 271 people