Answer:
Step-by-step explanation:
The expression that you want to simplify is:
This is the simplification step-by-step:
1. Mulitply the expressions on the numerator among them and the expressions on the denominator among them:
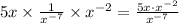
2. For equal bases that are multiplying, add the exponents:
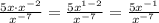
3. Pass the power on the denominator to the numerator by changing its sign (negative exponents become positive when inverted)
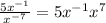
4. Simplify adding the exponents with the same base:
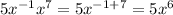
And that is the final expression in its most simple form.