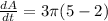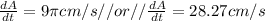Question

asked Sep 10, 2020 229k views

1 Answer

Silviu Burcea · Answer 1 · 2020-09-15T03:15:43+0000

Answer:

28.27 cm/s

Explanation:

Though Process:

The punch glass (call it bowl to have a shape in mind) is in the shape of a hemisphere
the radius
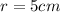
Punch is being poured into the bowl
The height at which the punch is increasing in the bowl is
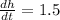
the exposed area is a circle, (since the bowl is a hemisphere)
the radius of this circle can be written as

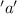
what is being asked is the rate of change of the exposed area when the height
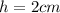
the rate of change of exposed area can be written as
.
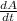since the exposed area is changing with respect to the height of punch. We can use the chain rule:

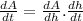
and since
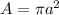$A = \pi a^2$ the chain rule above can simplified to
-- we can call this Eq(1)

Solution:

the area of the exposed circle is

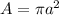
$A =\pi a^2$

the rate of change of this area can be, (using chain rule)

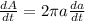$(dA)/(dt) = 2 \pi a (da)/(dt)$ we can call this Eq(2)

what we are really concerned about is how
changes as the punch is being poured into the bowl i.e
(da)/(dh)

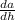
So we need another formula: Using the property of hemispheres and pythagoras theorem, we can use:

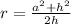
r = (a^2 + h^2)/(2h)

and rearrage the formula so that a is the subject:

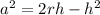
a^2 = 2rh - h^2

now we can derivate a with respect to h to get
(da)/(dh)

2a (da)/(dh) = 2r - 2h

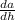
simplify

(da)/(dh) = (r-h)/(a)

we can put this in Eq(1) in place of
(da)/(dh)

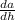
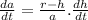
(da)/(dt) = (r-h)/(a) . (dh)/(dt)

and since we know
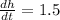
(dh)/(dt) = 1.5

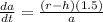
(da)/(dt) = ((r-h)(1.5))/(a)

and now we use substitute this
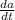(da)/(dt) . in Eq(2)

$(dA)/(dt) = 2 \pi a ((r-h)(1.5))/(a)$

simplify,

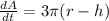
$(dA)/(dt) = 3 \pi (r-h)$

This is the rate of change of area, this is being asked in the quesiton!

Finally, we can put our known values:

r = 5cm

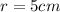
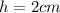h = 2cm from the question

$(dA)/(dt) = 3 \pi (5-2)$

$(dA)/(dt) = 9 \pi cm/s// or//(dA)/(dt) = 28.27 cm/s$

Please log in or register to add a comment.