Question

The average price of homes sold in the U.S. in the past year was $220,000. A random sample of 81 homes sold this year showed a sample mean price of $210,000. It is known that the standard deviation of the population is $36,000. Using a 1% level of significance, test to determine if there has been a significant decrease in the average price homes. Use the p value approach. Make sure to show all parts of the test, including hypotheses, test statistic, decision rule, decision and conclusion.

Answer 1

We conclude that there has been a significant decrease in the average price homes.

Explanation:

We are given the following in the question:

Population mean, μ = $220,000

Sample mean,
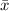`\bar{x}` = $210,000

Sample size, n = 81

Significance level, α = 0.051

Population standard deviation, σ = $36,000

First, we design the null and the alternate hypothesis

`H_(0): \mu = 220000\text{ dollars}\\H_A: \mu < 210000\text{ dollars}`

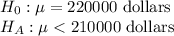
We use One-tailed z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

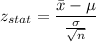
Putting all the values, we have

`z_(stat) = \displaystyle(210000 - 220000)/((36000)/(√(81)) ) = -2.5`

Calculating the p-value from the z-table, we have:

P-value = 0 .00621

Since,

P-value < Significance level

We reject the null hypothesis and accept the alternate hypothesis. Thus, there has been a significant decrease in the average price homes.