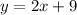Answer:
Step-by-step explanation:
Slope of line passing through (a,b) and (c,d) =

⇒ Slope of line passing through (-3, -4) and (1, 4) =
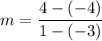
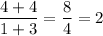
i.e. Slope of line passing through (-3, -4) and (1, 4) = 2
We know that the slopes of two parallel lines are equal.
Therefore , the slope of line parallel to the line passing through the points (-3, -4) and (1, 4)= 2
Also, equation of line passing through point (a,b) and has slope m :
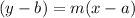
Then, the equation of line passing through point (-1, 7) and has slope 2 :
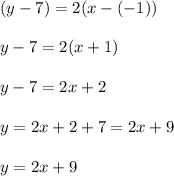
Hence, the required equation of the line that passes through the point (-1, 7) and is parallel to the line passing through the points (-3, -4) and (1, 4).