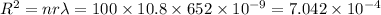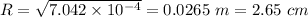Question

A piece of curved glass has a radius of curvature of r = 10.8 m and is used to form Newton's rings, as in the drawing. Not counting the dark spot at the center of the pattern, there are one hundred dark fringes, the last one being at the outer edge of the curved piece of glass. The light being used has a wavelength of 652 nm in vacuum. What is the radius R of the outermost dark ring in the pattern? (Hint: Note that r is much greater than R, and you may assume that tan(θ) = θ for small angles, where θ must be expressed in radians.)

Answer 1

Radius of the outer most dark fringe is 2.65 cm

Solution:

As per the question:

Radius of curvature of the glass, r = 10.8 m

No. of dark fringes, n = 100

Wavelength of light,
`\lambda = 652\ nm = 652* 10^(- 9)\ m`

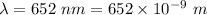
Now,

To calculate the radius R of the outermost ring:

Radius of the dark fringe of nth order is given by:

`R^(2) = nr\lambda = 100* 10.8* 652* 10^(- 9) = 7.042* 10^(- 4)`

`R = \sqrt{7.042* 10^(- 4)} = 0.0265\ m = 2.65\ cm`