150 different committees are possible
Solution:
Given that a student dance committee is to be formed consisting of 2 boys and 4 girls
The membership is to be chosen from 5 boys and 6 girls
To find : number of different possible committees
A combination is a selection of all or part of a set of objects, without regard to the order in which objects are selected
The formula for combination is given as:
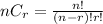
where "n" represents the total number of items, and "r" represents the number of items being chosen at a time
We have to select 2 boys from 5 boys
So here n = 5 and r = 2
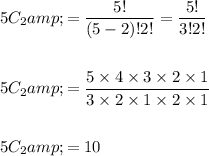
We have to select 4 girls from 6 girls
Here n = 6 and r = 4
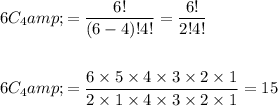
Committee is to be formed consisting of 2 boys and 4 girls:
So we have to multiply
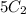 and
and
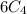
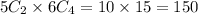
So 150 different committees are possible