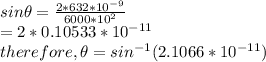Question

Monochromatic light from a helium-neon laser of wavelength of 632.8 nm is incident normally on a diffraction grating containing 6000 lines/cm. Find the angles at which one would observe the first order maximum, the second-order maximum, and so forth.

Answer 1

first-order maximum:\theta=sin^{-1}(0.10533*10^{-11} )

second-order maximum:\theta=sin^{-1}(2.1066*10^{-11} )

Explanation:

• here, maximum means bright fringes

• FORMULA :for bright fringes, we know that dsin
  `\theta`=n
  `\lambda`

(refer the diagram uploaded in the attachment)

• here,
  `[tex]\lambda= 632.8*10^(-9) meters \\d=6000*10^(2) lines/meter`

• for first order maximum, n=1

by substituting these values in the above formula,

`sin\theta=(1*632*10^(-9) )/(6000*10^(2) ) \\ =0.10533*10^(-11) \\therefore, \theta=sin^(-1)(0.10533*10^(-11)  )\\`

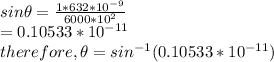
• for second order maximum, n=2

`sin\theta=(2*632*10^(-9) )/(6000*10^(2) ) \\ =2*0.10533*10^(-11) \\therefore, \theta=sin^(-1)(2.1066*10^(-11)  )`