Question

Chapter 38, Problem 001

Monochromatic light (that is, light of a single wavelength) is to be absorbed by a sheet of a certain material. Photon absorption will occur if the photon energy equals or exceeds 0.42 eV, the smallest amount of energy needed to dissociate a molecule of the material.

(a) What is the greatest wavelength of light that can be absorbed by the material?
(b) In what region of the electromagnetic spectrum is this wavelength located?

Answer 1

a)
`\lambda=2.95x10^(-6)m`

b) infrared region

Step-by-step explanation:

Photon energy is the "energy carried by a single photon. This amount of energy is directly proportional to the photon's electromagnetic frequency and is inversely proportional to the wavelength. If we have higher the photon's frequency then we have higher its energy. Equivalently, with longer the photon's wavelength, we have lower energy".

Part a

Is provide that the smallest amount of energy that is needed to dissociate a molecule of a material on this case 0.42eV. We know that the energy of the photon is equal to:

`E=hf`

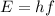
Where h is the Planck's Constant. By the other hand the know that
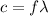`c=f\lambda` and if we solve for f we have:

`f=(c)/(\lambda)`

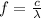
If we replace the last equation into the E formula we got:

`E=h(c)/(\lambda)`

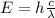
And if we solve for
`\lambda` we got:

`\lambda =(hc)/(E)`

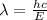
Using the value of the constant
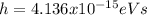`h=4.136x10^(-15) eVs` we have this:

`\lambda=(4.136x10^(15)eVs (3x10^8 (m)/(s)))/(0.42eV)=2.95x10^(-6)m`

`\lambda=2.95x10^(-6)m`

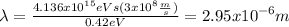
Part b

If we see the figure attached, with the red arrow, the value for the wavelenght obtained from part a) is on the infrared region, since is in the order of
`10^(-6)m`