Answer:
0.546 is the probability that a randomly selected smartphone users in the age range 11 to 55+ is between 30 and 54 years old.
Explanation:
We are given the following information in the question:
Mean, μ = 34.8 years
Standard Deviation, σ = 14.1 years
We are given that the distribution of ages of smartphone is a bell shaped distribution that is a normal distribution.
Formula:
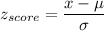
P( age range is between 30 and 54 years old)
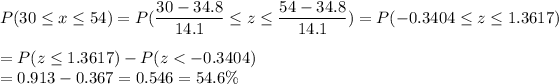
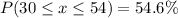
0.546 is the probability that a randomly selected smartphone users in the age range 11 to 55+ is between 30 and 54 years old.