Question

1. Twenty-four people go on holidays. If 15 go swimming, 12 go fishing, and 6 do neither,

how many go swimming and fishing? Draw a Venn diagram and fill in the number of

people in all four regions​

Answer 1

9 people went swimming and fishing.

Explanation:

We solve this question building a Venn Diagram.

We have that:

In total, there are 24 people.

6 do neither of these activities.

x go both swimming and fishing.

15 go swimming. This included those who go both swimming and fishing, so for the addition, we consider those who only go swimming, which is given by 15 - x.

12 go fishing, of which 12 - x only go fishing, by the same logic as above.

How many go swimming and fishing?

This in x

Adding all(neither, both swimming and fishing, only swimming, only fishing), we get 24. So

`6 + x + 15 - x + 12 - x = 24`

`33 - x = 24`

`x = 9`

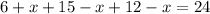
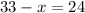
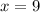
9 people went swimming and fishing.