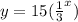Question

PLEASE HELP ME ITS ALREADY LATE AND ITS BRINGIN MY GRADE WAY DOWN PLEASE HEPL ME!!!!

The following graph is of an exponential function of the form y=a*bx.
What values of a and b would make this equation work?
a=
b=

Answer 1

`a=15`

`b=(1)/(3)`

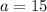
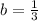
Explanation:

we have an exponential function of the form

`y=a(b^x)`

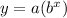
where

a is the initial value or y-intercept

b is the base

Looking at the graph

we can see the ordered pairs (0,15) and (1,5)

(0,15) ---> y-intercept

so

The value of a is equal to

`a=15`

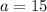
substitute

`y=15(b^x)`

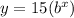
with the point (1,5) find the value of b

For x=1, y=5

substitute in the exponential function

`5=15(b^1)`

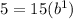
solve for b

`5=15(b)`

`b=(1)/(3)`

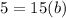
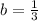
therefore

The exponential function is

`y=15((1)/(3)^x)`