Question

Given f(x) = x^2 – 3 and g(x) = x+2/x . Find (g ° f)(4).

A. 11/13
B. 6
C. 15/13
D. -6

Answer 1

C

Explanation:

Given the two functions, we need to find

(g ° f)(4)

This means, we need to put the function f(x) INTO the function g(x) and then evaluate that new function at x = 4.

We put the whole expression of f(x) into "x" of g(x). Shown below:

`f(x)=x^2-3\\g(x)=(x+2)/(x)\\(gof)(x)=(x^2-3+2)/(x^2-3)\\(gof)(x)=(x^2-1)/(x^2-3)`

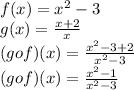
Now we plug in 4 into x and evaluate:

`(gof)(x)=(x^2-1)/(x^2-3)\\(gof)(4)=(4^2-1)/(4^2-3)\\(gof)(4)=(15)/(13)`

Thus,

correct answer is C