Question

What is the sum of the multiples of 3 between 100 and 1000

Answer 1

165150 is the sum of the multiples of 3 between 100 and 1000.

Explanation:

We need to find the sum of multiples of 3 between 100 and 1000.

First we will find the Total number of multiples of 3 between 100 and 1000.

Let a be the first multiple and l be the last multiple of 3

100 is not the multiple of 3.

101 is not the multiple of 3.

102 is the multiple of 3.

Hence first term a = 102

Similarly.

1000 is not a multiple of 3

999 is a multiple of 3

hence last term l = 999

Also d is the common difference.

hence d = 3.

Now by using Arithmetic progression formula we get;

`T_n(l) =a+(n-1)d\\ 999=102+(n-1)3\\999-102=(n-1)3\\897=(n-1)3\\(897)/(3)=n-1\\\\n-1=299\\n=299+1\\n=300`

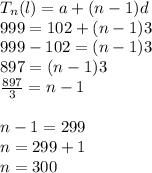
Hence there are 300 multiples of 3 between 100 and 1000

Now n=300, a=102, l = 999

Hence to find the sum of all the multiples we use the Sum of n terms in AP formula;

Sum of n term
`S_n= (n)/(2)(a+l)`

`S_(300)= (300)/(2)(102+999)\\\\S_(300)= 150(102+999)\\S_(300)= 150* 1101\\S_(300)= 165150`

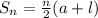
Hence,165150 is the sum of the multiples of 3 between 100 and 1000.