Question

Be sure to answer all parts. List the evaluation points corresponding to the midpoint of each subinterval to three decimal places, sketch the function and approximating rectangles and evaluate the Riemann sum to six decimal places if needed. f(x) = x2 + 4,[4, 5], n = 4. Give your answer in an ascending order. Evaluation points: , ,

Answer 1

The Riemann Sum for
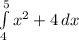`\int\limits^5_4 {x^2+4} \, dx` with n = 4 using midpoints is about 24.328125.

Explanation:

We want to find the Riemann Sum for
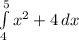`\int\limits^5_4 {x^2+4} \, dx` with n = 4 using midpoints.

The Midpoint Sum uses the midpoints of a sub-interval:

`\int_(a)^(b)f(x)dx\approx\Delta{x}\left(f\left((x_0+x_1)/(2)\right)+f\left((x_1+x_2)/(2)\right)+f\left((x_2+x_3)/(2)\right)+...+f\left((x_(n-2)+x_(n-1))/(2)\right)+f\left((x_(n-1)+x_(n))/(2)\right)\right)`

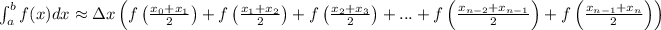
where
`\Delta{x}=(b-a)/(n)`

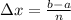
We know that a = 4, b = 5, n = 4.

Therefore,
`\Delta{x}=(5-4)/(4)=(1)/(4)`

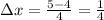
Divide the interval [4, 5] into n = 4 sub-intervals of length
`\Delta{x}=(1)/(4)`

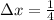
`\left[4, (17)/(4)\right], \left[(17)/(4), (9)/(2)\right], \left[(9)/(2), (19)/(4)\right], \left[(19)/(4), 5\right]`

Now, we just evaluate the function at the midpoints:

`f\left((x_(0)+x_(1))/(2)\right)=f\left((\left(4\right)+\left((17)/(4)\right))/(2)\right)=f\left((33)/(8)\right)=(1345)/(64)=21.015625`

`f\left((x_(1)+x_(2))/(2)\right)=f\left((\left((17)/(4)\right)+\left((9)/(2)\right))/(2)\right)=f\left((35)/(8)\right)=(1481)/(64)=23.140625`

`f\left((x_(2)+x_(3))/(2)\right)=f\left((\left((9)/(2)\right)+\left((19)/(4)\right))/(2)\right)=f\left((37)/(8)\right)=(1625)/(64)=25.390625`

`f\left((x_(3)+x_(4))/(2)\right)=f\left((\left((19)/(4)\right)+\left(5\right))/(2)\right)=f\left((39)/(8)\right)=(1777)/(64)=27.765625`

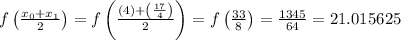
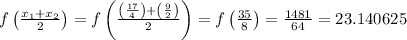
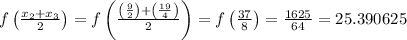
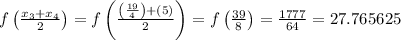
Finally, use the Midpoint Sum formula

`(1)/(4)(21.015625+23.140625+25.390625+27.765625)=24.328125`

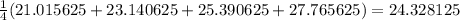
This is the sketch of the function and the approximating rectangles.