Question

PLEASE HELP ME!!!!!!! I AM NOT GOOD AT MATH!

Given the function f(x)= \frac{x^2+7x+10}{x^2+9x+20} Describe where the function has a hole and how you found your answer.

Answer 1

Only hole of function
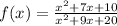`f(x) = (x^(2)+7x+10 )/(x^(2)+9x+20 )` is at x=(-4)

Explanation:

Given the function is
`f(x) = (x^(2)+7x+10 )/(x^(2)+9x+20 )`

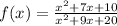
In order to find holes of any function, you should find when function is becoming undefined or say " infinity"

Given function is polynomial function.

It will become undefined become denominator become zero

`x^(2)+9x+20=0`

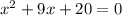
Solving for x value when denominator become zero

`x^(2)+9x+20=0\\x^(2)+5x+4x+20=0\\x(x+5)+4(x+5)=0\\(x+4)(x+5)=0`

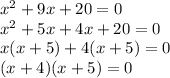
we get possible holes at x=(-4) and x=(-5)

Check whether you can eliminate any holes

Now, Solving for x value when numerator become zero

`x^(2)+7x+10=0\\x^(2)+5x+2x+10=0\\(x+5)(x+2)=0`

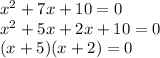
x=(-5) and x=(-2)

x=(-5) is common is both numerator and denominator.

So that, we can eliminate it.

`f(x) = ((x+5)(x+2))/((x+5)(x+4))`

`f(x) = ((x+2))/((x+4))`

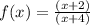
Therefore, Only hole of function
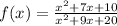`f(x) = (x^(2)+7x+10 )/(x^(2)+9x+20 )` is at x=(-4)