Question

Two UFPD are patrolling the campus on foot. To cover more ground, they split up and begin walking in different directions. Office A is walking at 5 mph directly south while Office B is walking at 6 mph directly west. How long would they need to walk before they are 2 miles away from each other?

Answer 1

0.256 hours

Step-by-step explanation:

Vectors in the plane

We know Office A is walking at 5 mph directly south. Let
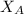`X_A` be its distance. In t hours he has walked

`X_A=5t\ \text{miles}`

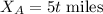
Office B is walking at 6 mph directly west. In t hours his distance is

`X_B=6t\ \text{miles}`

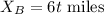
Since both directions are 90 degrees apart, the distance between them is the hypotenuse of a triangle which sides are the distances of each office

`D=√(X_A^2+X_B^2)`

`D=√((5t)^2+(6t)^2)`

`D=√(61)t`

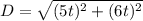
This distance is known to be 2 miles, so

`√(61)t=2`

`t =(2)/(√(61))=0.256\ hours`

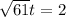
t is approximately 15 minutes