Question

Use the Distributive property to expand the expression y(9-0.2x)

Answer 1

The expression y(9-0.2x) expands to 9y - 0.2xy using the distributive property, where y is multiplied by each term inside the parentheses.

Step-by-step explanation:

To expand the expression y(9-0.2x) using the distributive property, you multiply y by each term inside the parentheses. Applying the distributive property, we get:

y × 9 - y × 0.2x

Which simplifies to:

9y - 0.2xy

This is the expanded form of the given expression.

Answer 2

9y - 0.2xy is the answer after applying Distributive property.

Step-by-step explanation:

Given:

`y(9-0.2x)`

To Find:

Expression after applying Distributive property.

Solution:

Distributive property:

In Distributive property, it lets you multiply a sum by multiplying each addend separately and then add the products.

OK, that definition is not really helpful for most people. It is easier to understand the meaning if you look at the examples below.

i.e A (B + C) = A×B + A×C

On Applying Distributive property to the given expression we get,

`y(9-0.2x)=y* 9-y*0.2* x\\y(9-0.2x)=9y-0.2* x* y`

`\therefore y(9-0.2x)=9y-0.2xy \ \ \ \textrm{we can write xy or yx it same as 2*3 = 3*2 = 6}`

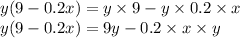
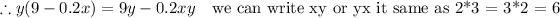
9y - 0.2xy

is the answer after applying Distributive property.