Question

The door is 3.00 m tall and 1.25 m wide, and it weighs 750 N . You can ignore the friction at the hinges. If Exena applies a force of 220 N at the edge of the door and perpendicular to it, how much time does it take her to close the door?

Answer 1

0.674 s = t

Step-by-step explanation:

Assuming that the door is completely open, exena need to rotate the door 90°.

Now, using the next equation:

T = I∝

Where T is the torque, I is the moment of inertia and ∝ is the angular aceleration.

Also, the torque could be calculated by:

T = Fd

where F is the force and d is the lever arm.

so:

T = 220N*1.25m

T = 275 N*m

Addittionaly, the moment of inertia of the door is calculated as:

I =
`(1)/(3)Ma^2`

where M is the mass of the door and a is the wide.

I =
`(1)/(3)(750/9.8)(1.25)^2`

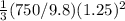
I = 39.85 kg*m^2

Replacing in the first equation and solving for ∝, we get::

T = I∝

275 = 39.85∝

∝ = 6.9 rad/s

Now, the next equation give as a relation between θ (the angle that exena need to rotate) ∝ (the angular aceleration) and t (the time):

θ =
`(1)/(2)`∝
`t^2`

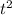
Replacing the values of θ and ∝ and solving for t, we get:

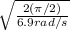`\sqrt{(2(\pi/2))/(6.9 rad/s)}` = t

0.674 s = t