Question

Find the equation of the line joining the points whose x coordinates on the curve y = 2x^2 - 3 are -1 and 1.​

Answer 1

The equation of the line joining the points (-1,-1), (1,-1) is

y +1 =0

Explanation:

Step(i):-

Given curve y = 2 x² -3 , x = -1 and x=1

substitute x =-1 in given curve y = 2 x² -3

y = 2 (-1 )² - 3

y = 2 -3

y = - 1

First point A( -1 ,-1)

substitute x =1 in given curve y = 2 x² -3

y = 2 (1)² - 3

y = -1

Second point B( 1 , -1 )

Step(ii):-

A( -1, -1 ) and B( 1,-1)

slope of the line

`m = (y_(2)-y_(1) )/(x_(2) -x_(1) ) = (-1-(-1))/(1-(-1)) =0`

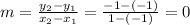
The equation of the straight line passing through the point ( -1,-1 ) having slope m =0

y - y₁ = m ( x - x₁ )

y - (-1) = 0( x-(-1)

y +1 =0

The equation of the line joining the points (-1,-1), (1,-1) is y +1 =0