Question

Beth bought 20 tickets to a movie, where adult tickets cost $8.00 and senior citizen tickets cost $4.00. She spent a total of $140. Which system of equations will determine the number of adult tickets, a, and the number of senior citizen tickets, s, Beth purchased?

Answer 1

The Total number of adults ticket's is 15

The Total number of Senior citizen ticket's is 5

Explanation:

Given as :

The total number of movies tickets were bought = 20

The cost of adults tickets = $ 8.00

The cost of senior citizen tickets = $ 4.00

The total money spent on movie tickets = $ 140

Let The total number of adults tickets = A

And The total number of senior citizen tickets = S

Now, According to question

The total number of movies tickets were bought = 20

I.e The total number of adults tickets + The total number of senior citizen tickets = 20

Or, A + S = 20

And $ 8 A + $ 4 S = $ 140 .........1

I.e 8 × ( A + S ) = 8 × 20

Or, 8 A + 8 S = 160 .......2

Solving the equation 1 and 2

Or, ( 8 A + 8 S ) - ( 8 A + 4 S ) = 160 - 140

Or, ( 8 A - 8 A ) + ( 8 S - 4 S ) = 20

or, 0 + 4 S = 20

∴ S =
`(20)/(4)`

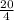
I.e S = 5

So, The number of Senior citizen ticket's = 5

Put The value of S in eq 1

So, 8 A + 4 × 5 = 140

Or, 8 A = 140 - 20

Or, 8 A = 120

∴ A =
`(120)/(8)`

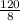
I.e A = 15

So, The number of adult's tickets = 15

Hence The Total number of adults ticket's is 15

And The Total number of Senior citizen ticket's is 5 Answer