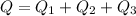Answer:209.98 kJ
Step-by-step explanation:
mass of water
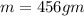
Initial Temperature of Water

Final Temperature of water
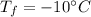
specific heat of ice

Latent heat

specific heat of water
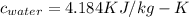
Heat require to convert water at
 to
to
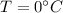
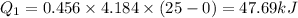
Heat require to convert water at
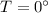 to ice at
to ice at
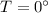
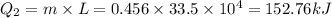
heat require to convert ice at

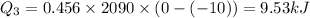
Total heat