Question

7

Overview
Home Pro
Question Progress
Here are two similar rectangles,
1 cm
2 cm
4 cm
Work out the area of the larger rectangle.

Answer 1

Given:

Two similar rectangles.

To find:

The area of the larger rectangle.

Solution:

Let x be the other side of the larger rectangle.

Corresponding sides of similar figures are always congruent.

`(x)/(1)=(4)/(2)`

`x=2`

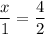
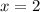
The other side of larger rectangle is 2 cm.

We know that, area of rectangle is

`Area=Length* Width`

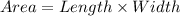
So, area of the larger rectangle is

`Area=4* 2`

`Area=8`

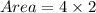
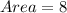
Therefore, the area of the larger rectangle is 8 sq. cm.