Question

A toy car having mass m = 1.10 kg collides inelastically with a toy train of mass M = 3.55 kg. Before the collision, the toy train is moving in the positive x-direction with a velocity of Vi = 2.20 m/s and the toy car is also moving in the positive x-direction with a velocity of vi = 4.95 m/s. Immediately after the collision, the toy car is observed moving in the positive x-direction with a velocity of 1.80 m/s.

(a) Determine the final velocity of the toy train. cm/s
(b) Determine the change ake in the total kinetic energy.

Answer 1

`V_(ft)= 317 cm/s`

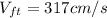
ΔK = 2.45 J

Step-by-step explanation:

a) Using the law of the conservation of the linear momentum:

`P_i = P_f`

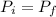
Where:

`P_i=M_cV_(ic) + M_tV_(it)`

`P_f = M_cV_(fc) + M_tV_(ft)`

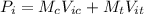
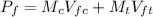
Now:

`M_cV_(ic) + M_tV_(it) = M_cV_(fc) + M_tV_(ft)`

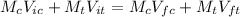
Where
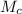`M_c` is the mass of the car,
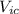`V_(ic)` is the initial velocity of the car,
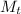`M_t` is the mass of train,
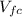`V_(fc)` is the final velocity of the car and
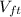`V_(ft)` is the final velocity of the train.

Replacing data:

`(1.1 kg)(4.95 m/s) + (3.55 kg)(2.2 m/s) = (1.1 kg)(1.8 m/s) + (3.55 kg)V_(ft)`

Solving for
`V_(ft)`:

`V_(ft)= 3.17 m/s`

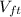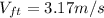
Changed to cm/s, we get:

`V_(ft)= 3.17*100 = 317 cm/s`

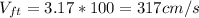
b) The kinetic energy K is calculated as:

K =
`(1)/(2)MV^2`

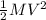
where M is the mass and V is the velocity.

So, the initial K is:

`K_i = (1)/(2)M_cV_(ic)^2+(1)/(2)M_tV_(it)^2`

`K_i = (1)/(2)(1.1)(4.95)^2+(1)/(2)(3.55)(2.2)^2`

`K_i = 22.06 J`

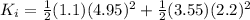
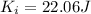
And the final K is:

`K_f = (1)/(2)M_cV_(fc)^2+(1)/(2)M_tV_(ft)^2`

`K_f = (1)/(2)(1.1)(1.8)^2+(1)/(2)(3.55)(3.17)^2`

`K_f = (1)/(2)(1.1)(1.8)^2+(1)/(2)(3.55)(3.17)^2`

`K_f = 19.61 J`

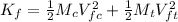
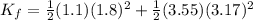
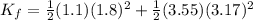
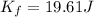
Finally, the change in the total kinetic energy is:

ΔK = Kf - Ki = 22.06 - 19.61 = 2.45 J