Question

If A = {x | x = 3n, n € {2,3,4}} and

B = {x x = 4m - 3, m = {1,2,3}},
what element exists in the
intersection of these two sets?

Answer 1

Answer: 9

====================================

Step-by-step explanation:

The intersection of the two sets is the list of all values that are in both sets at the same time.

Let's convert set A into roster notation. Roster notation means we just list out all the members (use ellipses if there are a lot of values you don't want to write out; luckily these sets are small). Plug n = 2 into x = 3n and you'll find that x = 6. Repeat for n = 3, and you get x = 9. Repeat for n = 4 and you get x = 12.

Set A looks like this: {6, 9, 12}

-------

Repeat the same basic steps for set B. We'll plug m = 1 into x = 4m-3 to get x = 1. Plug m = 2 into that same equation to get x = 5. Finally m = 3 leads to x = 9

Set B = {1, 5, 9}

-------

In summary,

A = {6, 9, 12}

B = {1, 5, 9}

We see that only 9 is in both sets at the same time.

Therefore,
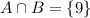`A \cap B = \left\{ 9 \right\}` which says "the intersection of set A and set B is the set { 9 } ".

The Venn Diagram shown below has the single element 9 in the overlapping region of the two circles. The other values are in their proper respective circles, but not inside the overlapping region. Set U is the universal set.