Question

A 200-Ω resistor is connected in series with a 10-µF capacitor and a 60-Hz, 120-V (rms) line voltage. If electrical energy costs 5.0¢ per kWh, how much does it cost to leave this circuit connected for 24 hours?

Answer 1

Cost to leave this circuit connected for 24 hours is $ 3.12.

Step-by-step explanation:

We know that,

`\mathrm{X}_{\mathrm{c}}=\frac{1}{2 \pi \mathrm{fc}}`

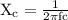
f = frequency (60 Hz)

c= capacitor (10 µF =
`10^-6`)

`\mathrm{X}_{\mathrm{c}}=\text { Capacitive reactance }`

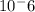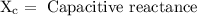
Substitute the given values

`\mathrm{X}_{\mathrm{c}}=(1)/(2 * 3.14 * 10 * 10^(-6) * 60)`

`\mathrm{X}_{\mathrm{c}}=(1)/(3.768 * 10^(-3))`

`\mathrm{x}_{\mathrm{c}}=265.39 \Omega`

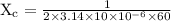
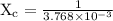
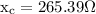
Given that, R = 200 Ω

`X^(2)=R^(2)+X c^(2)`

`X^(2)=200^(2)+265.39^(2)`

`X^(2)=40000+70431.85`

`X^(2)=110431.825`

`x=√(110431.825)`

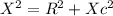
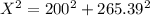
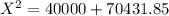
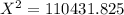
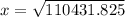
X = 332.31 Ω

`\text { Current }(I)=(V)/(R)`

`\text { Current }(I)=(120)/(332.31)`

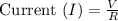
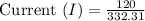
Current (I) = 0.361 amps

“Real power” is only consumed in the resistor,

`\mathrm{I}^(2) \mathrm{R}=0.361^(2) * 200`

`\mathrm{I}^(2) \mathrm{R}=0.1303 * 200`

`\mathrm{I}^(2) \mathrm{R}=26.06 \mathrm{Watts} \sim 26 \mathrm{watts}`

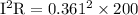
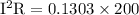
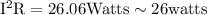
In one hour 26 watt hours are used.

Energy used in 54 hours = 26 × 24 = 624 watt hours

E = 0.624 kilowatt hours

Cost = (5)(0.624) = 3.12