Question

The half-life of the radioactive element krypton-91 is 10 seconds. If 16 grams of krypton-91 are initially present, how many grams are present after 35 seconds? A=A0ekt

Answer 1

1.415 gram of the element will be left.

Explanation:

The decay of radioactive element Krypton-91 can be formulated as

`A_(t) = A_(0) e^(-kt)` ............ (1)

where,
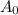`A_(0)` is the initial amount of the element.

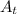`A_(t)` is the amount of element left after t seconds.

And k is a rate constant.

Now, given that the half-life of the element is 10 seconds.

So, from equation (1) we get

`0.5 = e^(- k * 10)`

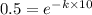
taking ln on both sides, we get.

ln 0.5 = -10k

⇒ k = 0.0693

So, the equation (1) becomes
`A_(t) = A_(0) e^(-0.0693t)` ........ (2)

Now, if 16 gram of the element are initially present, then we asked to determine the amount of the element left after 35 seconds.

So, from equation (2) we have
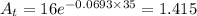`A_(t) = 16 e^(- 0.0693 * 35) = 1.415` gm.

So, 1.415 gram of the element will be left. (Answer)