Question

A spring of constant 20 N/m has compressed a distance 8 m by a(n) 0.3 kg mass, then released. It skids over a frictional surface of length 2 m with a coefficient of friction 0.16, then compresses the second spring of constant 2 N/m. The acceleration of gravity is 9.8 m/s2.

How far will the second spring compress in order to bring the mass to a stop?

Answer 1

`X_2=25.27m`

Step-by-step explanation:

Here we will call:

1.
`E_1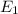`: The energy when the first spring is compress

2.
`E_2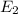`: The energy after the mass is liberated by the spring

3.
`E_3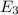`: The energy before the second string catch the mass

4.
`E_4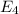`: The energy when the second sping compressed

so, the law of the conservations of energy says that:

1.
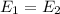
`E_1 = E_2`

2.
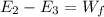
`E_2 -E_3= W_f`

3.
`E_3 = E_4`

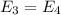
where
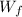`W_f` is the work of the friction.

1. equation 1 is equal to:

`(1)/(2)Kx^2 = (1)/(2)MV_2^2`

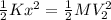
where K is the constant of the spring, x is the distance compressed, M is the mass and
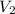`V_2` the velocity, so:

`(1)/(2)(20)(8)^2 = (1)/(2)(0.3)V_2^2`

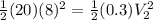
Solving for velocity, we get:

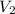`V_2` = 65.319 m/s

2. Now, equation 2 is equal to:

`(1)/(2)MV_2^2-(1)/(2)MV_3^2 = U_kNd`

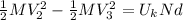
where M is the mass,
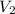`V_2` the velocity in the situation 2,
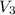`V_3` is the velocity in the situation 3,
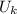`U_k` is the coefficient of the friction, N the normal force and d the distance, so:

`(1)/(2)(0.3)(65.319)^2-(1)/(2)(0.3)V_3^2 = (0.16)(0.3*9.8)(2)`

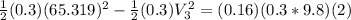
Volving for
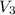`V_3`, we get:

`V_3 = 65.27 m/s`

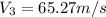
3. Finally, equation 3 is equal to:

`(1)/(2)MV_3^2 = (1)/(2)K_2X_2^2`

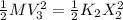
where
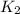`K_2` is the constant of the second spring and
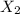`X_2` is the compress of the second spring, so:

`(1)/(2)(0.3)(65.27)^2 = (1)/(2)(2)X_2^2`

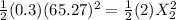
solving for
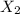`X_2`, we get:

`X_2=25.27m`