Question

In a health club, research shows that on average, patrons spend an average of 42.5 minutes on the treadmill, with a standard deviation of 5.4 minutes. It is assumed that this is a normally distributed variable.

Find the probability that randomly selected individual would spent between 30 and 40 minutes on the treadmill.

a)0.38

b)0.69

c)0.99

d)0.31

Answer 1

Answer: d) 0.31

Explanation:

Given : In a health club, research shows that on average, patrons spend an average of 42.5 minutes on the treadmill, with a standard deviation of 5.4 minutes.

i.e.
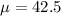`\mu=42.5` and
`\sigma= 5.4`

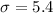
It is assumed that this is a normally distributed variable.

Let x denotes the time spend by a person on treadmill.

Then, the probability that randomly selected individual would spent between 30 and 40 minutes on the treadmill.

`P(30<x<40)=P((30-42.5)/(5.4)<(x-\mu)/(\sigma)<(40-42.5)/(5.4))\\\\\approxP(-2.31<z<0.46)\\\\=P(z<-0.46)-P(z<-2.31)\ \ [\because\ P(z_1<z<z_2)=P(z<z_2)-P(z<z_1)]\\\\=1-P(z<0.46)-(1-P(z\leq2.31))\ \ [\because P(Z>z)=1-P(Z\leq z)]\\\\=1-0.6772419-(1-0.9895559)\ \ \text{[By using z-table or calculator]}\\\\=0.3227581-0.0104441=0.312314\approx0.31`

Hence, the required probability = 0.31

Thus , the correct answer = d) 0.31