Question

A​ boat's crew rowed 7.5 miles​ downstream, with the​ current, in 1.5 hours. The return trip​ upstream, against the​ current, covered the same​ distance, but took 2.5 hours. Find the​ crew's average rowing velocity in still water and the average velocity of the current.

Answer 1

Average rowing velocity of boat in still water is 4 miles per hour and average velocity of the current is 1 mile per hour.

Explanation:

We are given the following in the question:

Let x be the average rowing velocity of boat in still water and y be the the average velocity of the current.

`\text{Speed} = \displaystyle\frac{\text{Distance}}{\texr{Time}}`

The boat rowed 7.5 miles​ downstream, with the​ current, in 1.5 hours.

Velocity with the current =

`=\text{average rowing velocity of boat in still water} + \text{ average velocity of the current} = x + y`

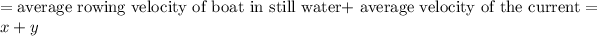
Thus, we can write the equation:

`7.5 = (x+y)1.5\\x+y = 5`

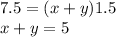
The return trip​ upstream, against the​ current, covered the same​ distance, but took 2.5 hours.

Velocity against the current =

`=\text{average rowing velocity of boat in still water} - \text{ average velocity of the current} = x - y`

Thus, we can write the equation:

`7.5 = (x-y)2.5\\x-y = 3`

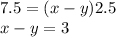
Solving, the two equations:

`2x = 8\\x = 4, y = 1`

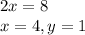
Thus, average rowing velocity of boat in still water is 4 miles per hour and average velocity of the current is 1 mile per hour.