Question

A soccer ball is thrown upward from the top of a 204 foot high building at a speed of 112 feet per second. The soccer ball's height above ground can be modeled by the equation . When does the soccer ball hit the ground?

Answer 1

8.5 seconds to hit the ground

Explanation:

A soccer ball is thrown upward from the top of a 204 foot high building at a speed of 112 feet per second.

`h(t)=-16t^2+V_0t+h_0`

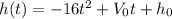
Vo is the speed 112 feet per second

h0 is the initial height = 204 foot

So the equation becomes

`h(t)=-16t^2+112t+204`

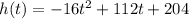
When the soccer ball hit the ground then the height becomes 0

`0=-16t^2+112t+204`

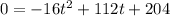
Apply quadratic formula

`x=(-b\pm √(b^2-4ac))/(2a)`

`t=(-112+√(112^2-4 (-16) \cdot 204))/(2(-16))`

`t=(-112+√(25600))/(-32)=-1.5`

`(-112-√(25600))/(-32)=8.5`

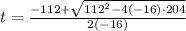
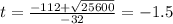
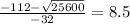
time cannot be negative

so it takes 8.5 seconds to hit the ground