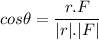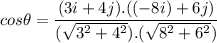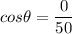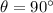Question

Force F = − + ( 8.00 N i 6.00 N j ) ( ) acts on a particle with position vector r = + (3.00 m i 4.00 m j ) ( ) .

What are

(a) the torque on the particle about the origin, in unit-vector notation
(b) the angle between the directions of r and F ?

Answer 1

Step-by-step explanation:

Given that,

Force,
`F=((-8i)+6j)\ N`

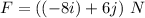
Position of the particle,
`r=(3i+4j)\ m`

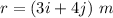
(a) The toque on a particle about the origin is given by :

`\tau=F* r`

`\tau=((-8i)+6j) * (3i+4j)`

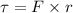
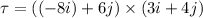
Taking the cross product of above two vectors, we get the value of torque as :

`\tau=(0+0-50k)\ N-m`

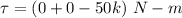
(b) Let
`\theta` is the angle between r and F. The angle between two vectors is given by :

`cos\theta=(r.F)/(|r|.|F|)`

`cos\theta=((3i+4j).((-8i)+6j))/((√(3^2+4^2) ).(√(8^2+6^2)) )`

`cos\theta=(0)/(50)`

`\theta=90^(\circ)`