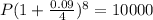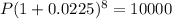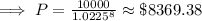Question

Two partners agree to invest equal amounts in their business. One will contribute​ $10,000 immediately. The other plans to contribute an equivalent amount in 2 years. How much should she contribute at that time to match her​ partner's investment​ now, assuming an interest rate of 9​% compounded quarterly​?

Answer 1

She should contribute $ 8369.38 ( approx )

Explanation:

Let P be the amount invested by the other partner,

∵ The amount formula in compound interest,

`A=P(1+(r)/(n))^(nt)`

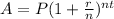
Where,

r = annual rate,

n = number of compounding periods in a year,

t = number of years,

Here, r = 9% = 0.09, n = 4 ( quarters in a year ), t = 2 years,

Then the amount after 2 years,

`A = P(1+(0.09)/(4))^(8)`

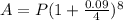
According to the question,

A = $ 10,000,

`P(1+(0.09)/(4))^(8)= 10000`

`P(1+0.0225)^8 = 10000`

`\implies P = (10000)/(1.0225^8)\approx \$ 8369.38`