Question

For fully developed laminar pipe flow in a circular pipe, the velocity profile is given by u(r) = 2 (1 - r2/R2) in m/s, where R is the inner radius of the pipe. Assuming that the pipe diameter is 3.1 cm, find the (a) maximum and (b) average velocities in the pipe as well as (c) the volume flow rate.

Answer 1

a)Uo= 2 m/s

b)
`u_(avg)=1 \ m/s`

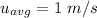
c)Q=7.54 x 10⁻⁴ m³/s

Step-by-step explanation:

Given that

`u(r)=2\left(1-(r^2)/(R^2)\right)`

Diameter ,D= 3.1 cm

Radius ,R= 1.55 cm

We know that in the pipe flow the general equation for laminar fully developed flow given as

`u(r)=U_o\left(1-(r^2)/(R^2)\right)`

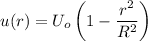
Uo=Maximum velocity

Therefore maximum velocity

Uo= 2 m/s

The average velocity

`u_(avg)=(U_o)/(2)`

`u_(avg)=(2)/(2)\ m/s`

`u_(avg)=1 \ m/s`

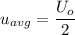
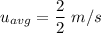
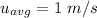
The volume flow rate

`Q=u_(avg). A`

`Q=\pi R^2* u_(avg)\ m^3/s`

`Q=\pi * (1.55* 10^(-2))^2* 1\ m^3/s`

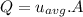
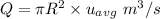
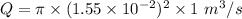
Q=0.000754 m³/s

Q=7.54 x 10⁻⁴ m³/s