Question

Samples of laboratory glass are in small, light packaging or heavy, large packaging. Suppose that 2% and 1% of the sample shipped in small and large packages, respectively, break during transit. If 53% of the samples are shipped in large packages and 47% are shipped in small packages, what proportion of samples break during shipment? Round your answer to four decimal places (e.g. 98.7654).

Answer 1

Answer: Our required probability is 0.0153.

Explanation:

Since we have given that

probability of sample shipped in small packages P(S) = 53% = 0.53

Probability of sample shipped in large packages P(L) = 47% = 0.47

Probability of sample in small break during transit P(S|B)= 2%=0.02

Probability of sample in large break during transit P(L|B) = 1% = 0.01

so, According to bayes theorem, we get that

Proportion of samples break during shipment is given by

`P(S).P(S|B)+P(L).P(L|B)\\\\=0.53* 0.02+0.47* 0.01\\\\=0.0153`

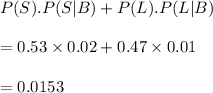
Hence, our required probability is 0.0153.