Question

A line is parameterized by x=8+6t x = 8 + 6 t and y=3+2t (a) Which of the following points are on the section of the line obtained by restricting t to nonnegative numbers (for each, enter Y if the point is on the section, and N if not)? (−4,−1): ___________ (26 , 9) :___________ (32,11): ___________ Then, give one more point that is on the section of the line obtained by this restriction:____________ (b) What are the endpoints of the line segment obtained by restricting t to − 5 ≤ t ≤ − 2 ? left endpoint: __________ right endpoint: _________

Answer 1

We have the line parametrized by

`x=8+6t\\y=3+2t`

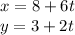
Solving for t in each equation we have that

`t=(x-8)/(6)\\t=(y-3)/(2)`

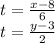
The point (a,b) lies in the line if when we replace a in the first equation and b in the second equation, the values of t coincide.

a)

1. (-4,-1)

`t=(-4-8)/(6)=-2\\t=(-1-3)/(2)=-2`

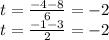
Then, (-4,-1) lies in the line but no lies in the section of the line obtained by restricting t to nonnegative numbers.

2. (26,9)

`t=(26-8)/(6)=3\\t=(9-3)/(2)=3`

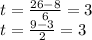
Since t is positive then (26,9) lies in the line and lies in the section of the line obtained by restricting t to nonnegative numbers.

3. (32,11)

`t=(32-8)/(6)=4\\t=(11-3)/(2)=4`

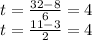
Since t is positive then (32,11) lies in the line and lies in the section of the line obtained by restricting t to nonnegative numbers.

4. If we take t=2 we obtain the point

`x=8+6(2)=20\\y=3+2(2)=7`

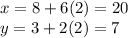
(20,7) that lies in the section of the line obtained by restricting t to nonnegative numbers.

b)

When t=-5,

`x=8+6(-5)=-22\\y=3+2(-5)=-7`

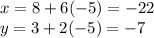
correspond to the point (-22,-7).

when t=-2

`x=8+6(-2)=-4\\y=3+2(-2)=-1`

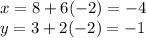
correspond to the point (-4,-1).

-22<-4 and -7<-1

then the left endpoint (-22,-7) and right endpoint (-4,-1)