Question

FASTTTTTTTTTTTTTTT PLEASEEEEEEEEEEEEE ITS 2O POINTS

The graph below shows a velocity vs. time graph. A graph with horizontal axis time (seconds) and vertical axis velocity (meters per second). A straight line runs from 0 seconds 10 meters per second to 5 seconds 2 meters per second. Which graph would match the same type of movement that the graph shows? A graph with horizontal axis time (seconds) and vertical axis position (meters). A straight line runs from 0 seconds 0 meters upward. A graph with horizontal axis time (seconds) and vertical axis position (meters). A concave line runs from 0 seconds 0 meters upward. A graph with horizontal axis time (seconds) and vertical axis position (meters). A straight line runs from 0 seconds some positive number meters upward downward to some positive number of seconds 0 meters. A graph with horizontal axis time (seconds) and vertical axis position (meters). A convex line runs downward from 0 seconds some positive number of meters to some positive number of seconds 0 meters.

Answer 1

Your answer is D) A graph with horizontal axis time (seconds) and vertical axis position (meters). A convex line runs downward from 0 seconds some positive number of meters to some positive number of seconds 0 meters.

Step-by-step explanation:

Answer 2

Answer is " A convex line runs downward from 0 seconds some positive number of meters to some positive number of seconds 0 meters. "

Step-by-step explanation:

The figure shows Velocity vs Time Graph.

At t1=0, u=10m/s

At t2=5, v=2m/s

Let's calculated the acceleration

`a=(v-u)/(t2-t1)`

`a=(2-10)/(5-0)`

`a=(-8)/(5)`

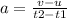
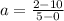
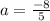
The equation of distance is given by

`d=ut+(a)/(2) t^(2)`

`d=(10)t+((-8)/(5))/(2) t^(2)`

`d=10t+(-8)/(10) t^(2)`

`d=10t+(-4)/(5) t^(2)`

`5d=50t-4t^(2)`

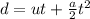
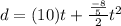
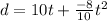
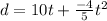
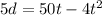
From here, You can plot the graph of above equation by taking several points.

When t=0,

`5d=50(0)-4(0)^(2) = 0m`

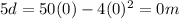
When t=5,

`5d=50(5)-4(5)^(2)`

`5d=250-100`

`5d=150`

`d=30m`

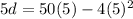
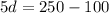
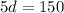
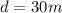
Similarly,

When t= 3s d=22.8m

When t=4s d=27.2m

Figure shown is graph of Distance vs Time.

Thus, answer is " A convex line runs downward from 0 seconds some positive number of meters to some positive number of seconds 0 meters. "